AI Unplugged 23: nGPT normalised transformer, LAUREL, TokenFormer

Insights over information

Table of Contents:

1. nGPT: Nomralised Transformer with Representation Learning

2. LAUREL: Learned Augmented Residual Layer

3. TokenFormer: Rethinking Transformer Scaling with Tokenized Model Parameters

Previous Edition

nGPT: NORMALIZED TRANSFORMER

TLDR:
 1. Normalised Transformer nGPT improves convergence and performance.
 2. Remove normalisation layers (RMSNorm and LayerNorm)
 3. Normalise weights (after backprop), all the intermediate outputs
 4. Different scaling for attention and MLP outputs

Normalization is foundational in machine learning, stabilizing training by controlling the scale of inputs and activations. This prevents issues like exploding and vanishing gradients. Traditionally, normalization is applied as an additional layer in neural networks. But what if normalization wasn’t just an add-on, but an inherent property of the model and its training? This is precisely what nGPT, the normalized Transformer, explores. In a way, nGPT is generalisation of Normalisation for neural networks aka making Normalisation Inherent to learning.

In a classical Transformer, in each layer, you’d have two key blocks namely, the Attention Block and the MLP. There’s a residual structure wherein, the output of each block is added to the input of the said block.

\(\begin{equation} \begin{split} h_A &= attn(RMSNorm(h)) \\ h &= h_A + h \\ h_M &= mlp(RMSNorm(h)) \\ h &= h + h_M \\ h &= RMSNorm(h) \\ \end{split} \end{equation}\)

Normalization, mathematically brings every vector to the surface of a hypersphere (hypersphere is the generalisation of a sphere in n-dimensions). Essentially, the magnitude of the said vectors would be equal to 1. So one can represent the vector with just its direction. So to go from a vector to its normalised form, you’d divide each of the components by the norm/magnitude of the entire vector.

Now how do you go from one vector (or point) to another? In a flat space, you’d just do linear interpolation LERP ie, take the weighted average of the two points with weights summing to 1. On a sphere, there’s a similar concept called Spherical Linear Interpolation SLERP. Intuitively, because everything on the sphere can be described by an angle, you can weighted average the angle between two points on sphere and consider the point arising from the resultant angle. But why do we care about this? Well to preserve the normalisation, we want to traverse along the surface of a given hypersphere. Mathematically speaking,

\(\begin{equation} \begin{split} LERP(\mathbf{a}, \mathbf{b}, \alpha) &= (1-\alpha) \mathbf{a} + \alpha \mathbf{b} \\ SLERP(\mathbf{a}, \mathbf{b}; \alpha) &= \frac{\sin((1 - \alpha)\theta)}{\sin(\theta)} a + \frac{\sin(\alpha\theta)}{\sin(\theta)} b \\ \text{ where } \theta = cos^{-1}(\mathbf{a}.\mathbf{b}) &= \text{angle between a and b} \end{split} \end{equation}\)

Off Topic: LERP-ing is a wonderful concept with wide range of applications including Game Development. If you are interested, I’d recommend watching this video from Freya Holmer on youtube. The animation below is from one of her tweets.

Now that we know how to interpolate between two points on a hypersphere, we know what to do with the residual equivalent for normalised transformer. This also gives us a clue on how to traverse on the hypersphere when we have a gradient (aka how to update the weights). But to simplify things, we don’t do SLERP but we stick to LERP. For small angles between a and b, (think of limit θ→0), SLERP is equivalent to LERP (aka any curve in small vicinity can be approximated by a line segment). As for why the angles are very small, we’ve discussed in our previous editions [1] how the input and output of the transformer layer/block are very similar. Armed with this information, we’d have the equations for nGPT. Here αA and αM are learnable parameters.

\(\begin{equation} \begin{split} h = Norm( h + \alpha_A (h_A - h)) \\ h = Norm( h + \alpha_M (h_M - h)) \\ \end{split} \end{equation}\)

Now that we’ve figured out the big picture, we need to zoom into micro details. In transformer, attention module consists of query, key, value weights and output projection. Similarly, MLP block has up, down and gate projections. How do you map those onto normalised architecture?

\(\begin{equation} \begin{split} q \leftarrow h W_q, \space k \leftarrow h W_k, \space v \leftarrow h W_v, \space \\ \text{Attention}(q, k, v) \leftarrow \text{softmax}\left(\frac{q k^\top}{\sqrt{d_k}} + M\right)v \\ h_A \leftarrow \text{Concat}(head_1, \ldots, head_{nheads}) W_o \end{split} \end{equation}\)

In case of nGPT, going the normalisation style, the weights Wq, Wk, Wv and Wo are normalised along the embedding dimension. This means, both vectors in Wx and the hidden states are on the hypersphere. Essentially the dot product here is equal to the cosine similarity as the magnitude of both are equal to 1. Hence the q,k,v are bound in [-1, 1]. But unfortunately, the product wouldn’t lie on a hypersphere. So we normalise the resultant as well.

\(\begin{equation} \begin{split} q \leftarrow \text{Norm}(q) s_{qk} \\ k \leftarrow \text{Norm}(k) s_{qk} \end{split} \end{equation}\)

You might be wondering why we have Sqk as the scaling factor? Well, if you remember, in the baseline transformer, we scale the product qk by 1/sqrt(dk). This is to ensure that the variance of the product is 1. Here, as the vectors are independently normalised before product, we’d need similar scaling factor to get the result back to unit norm.

Similarly, for MLP block, we have Wup, Wgate and Wdown. We do normalise them for nGPT.

\(\begin{equation} \begin{split} u \leftarrow h W_u, & \space \space g \leftarrow h W_g \\ h_M = SwiGLU(u, g) &W_{down} = (g . \sigma(g) * u) W_{down} \\ \text{for nGPT we have,} & u \leftarrow us_u, v \leftarrow vs_v \sqrt(d_{model}) \end{split} \end{equation}\)

To summarise, we have

• Remove normalisation layers like RMSNorm, LayerNorm

• Normalise all matrices, Wq, Wk, Wv, Wo, Wu, Wg, Wd, Embedding Ein and Eout.

• Use the update equations as mentioned above.

• Remove weight decay and learning rate warmup.

All this for what you ask? Well just like normalisation layers improve training and convergence, nGPT also improves convergence. Consistently across context lengths and across a couple of model sizes, the convergence happens much faster. We also see similar trend for down stream task performances. In fact, even the smaller 0.5B nGPT models outperform 1B baseline transformer.

validation loss as function of training tokens

downstream task performance

To understand why the drastic difference just by normalisation, we look at, you guessed it, Eigen values and their ratio. There’s a metric called condition number of matrices which is essentially the ratio of largest singular value to the smallest. A higher condition number means the matrix modifies the input significantly.

What we understand from this is, the initial weights in the baseline transformer’s attention module tends to modify the hidden states more drastically as compared to the later layers or even nGPT. Also, we observed in Differential Transformer blog that attention logits tend to go in the range of 300 while hidden states tend to go as high as 3000. Differential Transformer observed that their architecture results in reducing these and hence improve performance. Similarly, if we reduce the activation/hidden states to smaller scale, lesser gradient explosions, easier training and easier quantization too.

Another thing to note is, for nGPT we had different scale for attention block and MLP block namely, αA and αM. This differs from baseline transformer where the output of attention and MLP get equal weightage.

Just like Differential Transformer, nGPT is a cool new technique to improve upon transformers. One is yet to study how these architectures scale beyond the small 1B params. Any technique that improves the convergence speed or convergence limit without too many bells and whistles is always a welcome.

LAUREL: Learned Augmented Residual Layer

TLDR: 
  1. Modifying residual connections can improve neural networks
  2. Several ways to modify
    a. Add weighted sum of transformed and original components
    b. Linearly transform the original component and add it.
    c. Linearly transform all previous hidden states and weighted sum.
       Note that for b and c, linear transform can be low rank
  3. These techniques improve performance of models

Residual connections have been a key component in deep neural networks ever since ResNet. This is what enabled the models to grow deeper in size thus giving us wonderful stuff like GPT and whatnot. The key idea behind Residual connections is very simple. After any processing of the input, add the original input to the said output. Why you ask? Well let me explain

In neural networks, weights are generally initialised around 0. Be it normal distribution or uniform distribution, their mean generally is around zero. So the product of this weight matrix with the input would also result in something around zero. Essentially destroying the information that was previously created. So adding more layers after a point hurt the model performance back in those days.

Ideally speaking, because the weights are learnt and updated, one would in theory assume the weights to adapt so that the information in the input is not completely lost and hence has to be completely reconstructed. But another part of the problem is the gradients and weight decay which tend to again squish the weights. Now how do you solve it? Well, if the weights were initialised around Identity Matrix, the information would be preserved. Think of it, multiplying by something around Identity is equivalent to multiplying by something that is around zero and then adding the original input back. (Though there’s a minor difference that we add the input after applying non linearity). Here f(x) is the output of the layer (linear transformation)

\(y = g(x) = (I+f)x = (I + \Delta I) x = x + \Delta W x = x + f(x)\)

So since ResNet days, almost every network use Residual connections. It has been the holy grail. But now, its time to think about it again. Sort of give it the upgrade it deserves. But how do you modify addition? Well all this while, we’ve been treating the transformed part and the original input with equal weightage. What if we modify that? Also, what if we don’t add the previous hidden state as is, but somehow modify it? Maybe even include hidden states from previous layers? Well all these small things are what we explore today. Lets go one by one.

1. Residual Weights (LAUREL-RW): This is where you weighted-add transformed and non transformed inputs. Here α and β are learned parameters.

   \(x_{i+1} = \alpha f(x_i) + \beta x_i\)

2. Low Rank Version (LAUREL-LR): Here instead of just adding input, we linearly transform the input. W is a learned matrix. We can also decompose this into low rank components in the spirit of LoRA. Here we add xi at the end to preserve the residual nature. Without that, ABx would again be zero-ish.

   \( x_{i+1} = f(x_i) + \mathbf{W} x_i = f(x_i) + \mathbf{AB}x_i + x_i\)

3. Previous Activations Version (LAUREL-PA): Here, instead of just considering the last activation, we involve all the previous activations. Here γi are learned. h(x) is a liner transformation like above and can be approximated by Low rank version.

   \( x_{i+1} = f(x_{i}) + \sum_{j=0}^{i} \gamma_{j} \cdot \mathbf{h}(x_{j}) = \sum_{j=0}^{i} \gamma_{j} \cdot \mathbf{AB}(x_{j}) \)

Note that by adding a linear transformation, one would see increase in number of parameters. But by making them Low Rank, essentially, we’re reducing the number of additional parameters. All this for what you ask? Well it definitely has to come with performance gains to make it justifiable.

Performance of LAUREL for Image classification and text generation

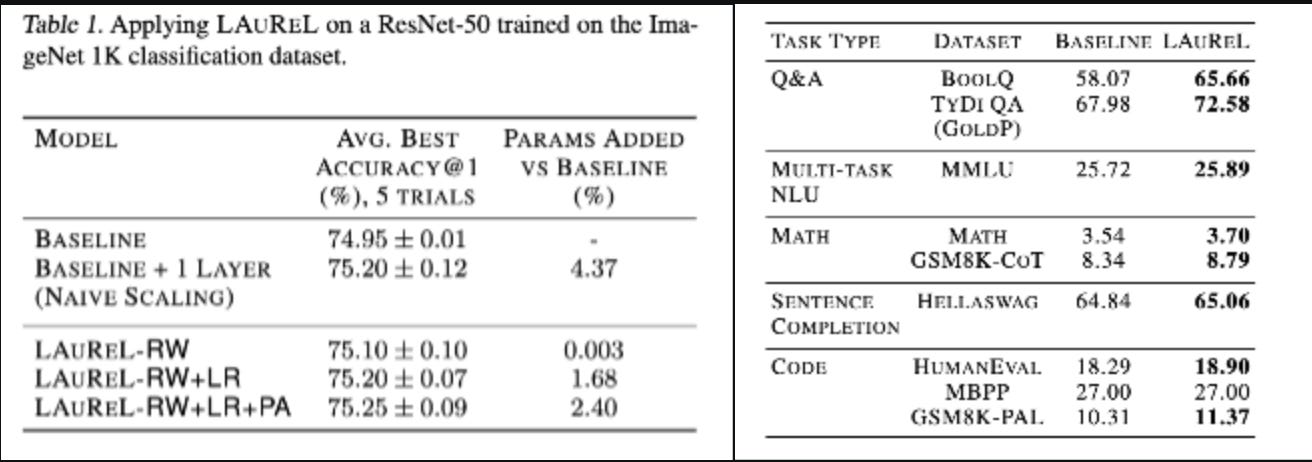
Indeed it does. We compare a 3B param LLM with and without LAUREL and the difference is quite visible. The same is the case for ResNet. There is also comparison to adding 1 more layer to ResNet which increases params by 4% but can’t outperform LAUREL-RW-LR with 1.69% additional params. Additionally it is also observed that the performance peaks when rank r=16 or 32.

Just like nGPT above, adding few more learnable parameters in place of just summation seems to help neural networks. nGPT had different addition scale for MLP and Attention blocks. Here too we have something similar. But insights into how α, β evolve over training would have been welcome.

TokenFormer: Rethinking Transformer Scaling

TLDR:
  1. Increasing size of transformers need complete retraining rendering
     small models' training unhelpful
  2. Attention blocks in transformers are input size agnostic. 
  3. Redefine token weight interactions as cross attention between
     tokens and parameters. This way params can be arbitrary size too.
  4. Adding new parameters would be like adding new param-tokens.

Transformers have revolutionized fields like NLP, visual tasks, and even 3D modeling with their flexible, scalable architecture. Typically, they handle two main interactions for each token: token-token (via the attention mechanism) and token-parameter (through linear projections). But as models keep growing, scaling them up becomes a heavy lift - it often means retraining everything from scratch.

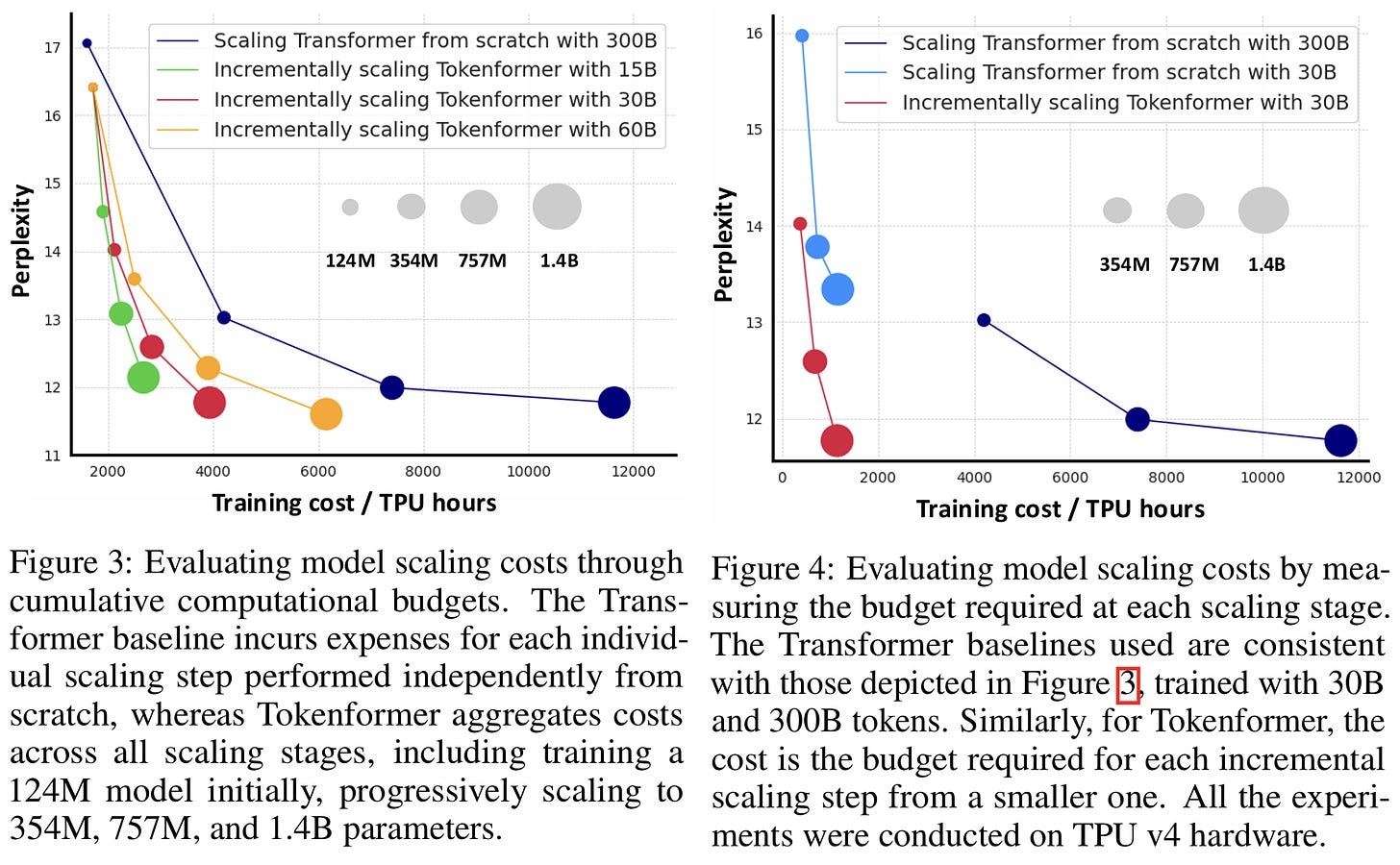
Here’s where TokenFormer steps in. This fresh architecture aims to make scaling smarter and more flexible. Instead of relying on the usual fixed projections, TokenFormer treats parameters as tokens themselves. This shift allows the model to grow incrementally by adding new "key-value" pairs, without the need for a full retraining. So, in practice, TokenFormer can expand (going from 124 million to 1.4 billion parameters, for example) while slicing training costs by over half.

Self-attention remains the heart of how transformers work. This mechanism lets the model capture relationships between tokens (words, pixels, or whatever input), no matter their sequence position. It relies on the classic "Q-K-V" projections—queries (Q), keys (K), and values (V) - that are derived from input tokens and handled by learnable weight matrices.

\(Q=X⋅W_Q,K=X⋅W_K,V=X⋅W_V\)

where 𝑊_𝑄, 𝑊_K, and 𝑊_𝑉 are learnable weight matrices. The interaction scores come from the dot product of Q and K, which then get normalized via softmax:

\(Attention(Q,K,V)=softmax(\frac{Q⋅K^T}{\sqrt d})⋅V\)

This design allows transformers to process variable-length input data and handle different types of tokens, making them highly versatile across applications.

Despite their power, transformers hit a scaling wall with the rising computational demands of self-attention. TokenFormer takes a fresh approach by introducing a Token-Parameter Attention layer (or "Pattention" layer) to streamline interactions and make scaling less resource-hungry. These so called parameters, with whom there’s a cross attention type of mechanism, are the scalable part.

TokenFormer’s twist is that it swaps out some of those traditional linear projections for the Pattention layer, letting certain tokens act as parameters. In the Pattention setup, input tokens interact with these parameter tokens through cross-attention, efficiently managing interactions without increasing other model dimensions (like channel count), which keeps computational costs in check. Here, two types of parameter tokens come into play: K_P (keys) and V_P​ (values):

\(Pattention(X, K_P, V_P) = \Theta (X.K^T_P). V_P \space\space\space\space \text{ where } \space\space\space\space\space \Theta_{i,j}(A) = f \left( \frac{ \tau \text{ x } A_{i,j} }{\sqrt {{\Sigma_{k=1}^{n}} A_{i,k}^2 }} \right)\)

where Θ is a modified softmax function optimized for the Pattention layer. f is a non linear function, which is set to GeLU in the paper.

By decoupling input and output dimensions, TokenFormer also supports incremental scaling without impacting other layers. The model layout remains familiar, with components like layer normalization (LN), multi-head attention (MHA), and feed-forward layers (FFN), but it swaps linear projections for Pattention layers. This design unifies token-token and token-parameter interactions through attention, treating both tokens and parameters as tokens - allowing a more streamlined, adaptable framework. Thanks to the flexible Pattention layer, TokenFormer scales by adding new key-value tokens to the existing set without needing to change the input-output dimensions - a technique similar to LoRA, letting the model keep its original knowledge while expanding its capacity. Initializing these new tokens at zero ensures continuity in training and speeds up convergence.

TokenFormer’s efficiency shines in various tasks. In "Progressive Model Scaling," for instance, it incrementally builds up by reusing weights from smaller models to initialize larger ones. Experiments on the OpenWebText dataset showed that TokenFormer achieved comparable performance to fully trained transformers but with notably less computational effort. Across language and visual tasks, it competes with top-tier models like Pythia in language benchmarks and Vision Transformers on ImageNet-1K. Gotta wait for “large” models though!

Ablation studies revealed tweaks that boost TokenFormer’s performance, especially in visual tasks. For example, swapping softmax for GeLU and using alternative normalization methods led to noticeable improvements. Additionally, replacing traditional normalization with a non-parametric version strengthened its modular, scalable design while maintaining performance. TokenFormer also broadens the Mixture-of-Experts (MoE) paradigm by treating each key-value parameter pair as an independent expert, making token-parameter interactions more efficient. This setup is ideal for tasks that need parameter-efficient tuning, as it lets you add parameter tokens for new tasks without a full retrain. The architecture also supports seamless integration across vision and language tasks, allowing models to align by merging key-value tokens from both modalities.