AI Unplugged 22: RoPE internals explained, Stuffed Mamba, Planning with Transfomer: Chess.
Insights over information.
Table of Contents:
Round and Round we go: What makes RoPE useful.
Stuffed Mamba: State Collapse and State Capacity of RNNs
Amortized Planning with Large-Scale Transformers: A Case Study on Chess
Round and Round we go: RoPE
TLDR:
1. RoPE is important. It gives models flexibility to attend to various patterns.
2. RoPE causes the learning to adapt and gives rise to higher norm at low frequency components (those that move slowly) and carry semantic information.
3. Similarly, high frequency components mostly carry attention to tokens x units apart.
4. One can construct arguably better position embeddings by truncating RoPE lower frequenciesTransformers by nature are order invariant. The attention operation, which takes weighted sum of values wouldn’t really care what order the previous tokens are in. But in language (even in images/videos) order plays a significant role. India defeated Australia is not the same as Australia defeated India. So how do we induce this order while training? The original attention paper tackled this by adding sinusoidal values to the token embeddings. The so called sinusoidal embeddings depended on what index the token is in, in the sentence.
But there was a problem. With architectures like sliding window attention, absolute position of the token in the sentence mattered less. So people explored alternatives to sinusoidal position embeddings. There came Rotary Position Embedding (RoPE) and AliBi. We even talked about Contextual Position Embedding (CoPE). It is safe to say that RoPE is the go to embedding for current LLMs. Take any popular LLM on huggingface and you’d find rope_theta in the config. So what is RoPE?
So instead of adding something to embeddings, imagine rotating queries and keys by angle proportional to their position in the sequence. So you rotate a query at i-th index by θi and the key at j-th is rotated by θj. So in a relative sense, the query is rotated θi - θj with respect to the query. So, essentially, RoPE only cares about how far is query from the key that too relative to the max length of the sequence. To be precise, for hidden dimension d, each component is rotated by an angle as follows. For further (mathematical) reading on RoPE we highly recommend Eleuther AI’s blog
So each vector (query or key) is split into d/2 components each consisting of 2 values. Those 2 values are rotated by the above said angle. So even in a single query vector (similarly key vector), the first 2 dimensions (components) are rotated by 1 radian higher than the the other components, for eg, the last 2 components are rotated by θ^(d-2)/d ~ 1/θ radians. And this is how much, two components of adjacent tokens relatively differ by and this adds up. So for tokens that are say m units apart, the first two components differ by m radians while the last two differ by ~m/θ radians. So there’s a notion of slow moving and fast moving components with RoPE.
Also remember that in attention, we perform dot product of query and key aka q.k (upto a transpose). Dot product of two vectors is bounded by the product of norms and is given by
So, dot product is maximised when q and k are along the same direction (angle b/w them is zero). But then when is attention with RoPE maximised? Well, the answer would be the same. When RoPE(q) and RoPE(k) are along the same direction. Given a query q, one can form a vector k for a given distance r such that attention is maximised. Namely, rotate every component of q by “-r” times the RoPE factors and use that as k (basically inverse of RoPE at distance r). Why is this important you ask? well, we might need to understand if RoPE has any monotonicity in terms of distance.
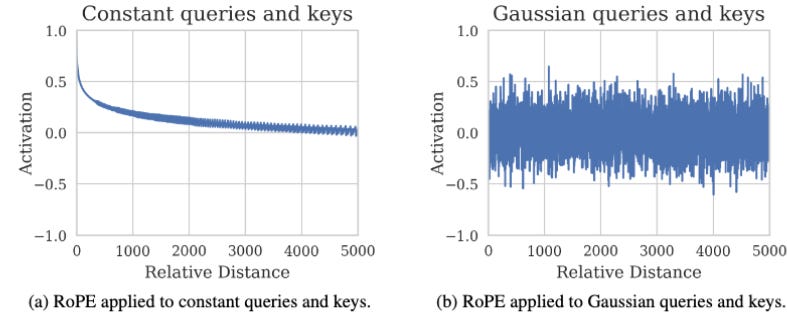
Next, we understand how RoPE effects a. constant queries and keys b. random queries and keys. Generally after training, the queries and keys fall somewhere between those two extremes.
So essentially, if queries and keys are same, RoPE Attention decreases with relative distance (farther the tokens are, lesser the attention activation with RoPE is). If the vectors are random, then there’s very little effect of distance on attention scores.
Now recollect what we previously mentioned about components moving fast and slow. Higher frequency components move so fast per token that the relative angle at any distance is very random in nature. This behaves pretty much like having two random vectors for query and key. On the other hand, for slow moving components, relative distance for a few positions, there’s not much rotation and hence dot product doesn’t die down to zero.
This asymmetry is something learning can exploit to form patterns, identify distances and a lot more. As shown below, upon learning, the norm of the lower frequency components is much higher than the higher frequency components. Essentially, majority of the attention weight would be coming from last few components.
If we observe gemma-7b’s component wise norm for specific attention heads (of layer 1), we notice that head 5 and 8 associate higher norm for high frequency components. This means, the attention score would be very sensitive to relative distance. So these heads end up acting as relative distance measurers aka attending to say something like previous token or self token.
On the other hand, low frequency components act as semantic components. These carry information. The disturbance due to relative distance is minimal (1/θ per token) and hence the information is not lost or corrupted. This begs the question. How far is too far for these low frequency components?
For something like llama-3.1-8B, they moved away from base theta of 10,000 and used 500,000. With a context length of 128k, if you want to attend to tokens separated by 128k units, the RoPE rotation would be θ*128k/2. At 1/10,000 this would be 6.4 radians or 2.04 rotations. This means somewhere in the middle there’s misalignment causing attention to go to 0. At 500,000, this total rotation would be 0.13 radians or 0.04 radians hence even the farthest of tokens only differ by a minuscule of angle. Hence semantic information is preserved (or say not destroyed by RoPE). Higher θ means one would need far too many tokens to destroy the semantic information.
With these insights in mind, can we construct a better position embedding scheme? Well think of it. If for most of the frequencies, the norm is low, there’s not much point in having so many high frequencies right (see the query-key mean norms image above). If we use more low frequencies, we can carry more semantic information.
On the other hand, if we set the low frequencies to zero, it should not hurt the model performance as rotation was not a very significant factor (0.13 radians as above) in attention computation. Ideally this should improve performance as query can perfectly attend to key separated by arbitrary distance without having to worry. Indeed this variant where lowest 25% frequencies are set to zero, outperforms RoPE and NoPE (No Positional Embeddings).
The paper also provides proofs as to why RoPE can attend to specific token patterns while NoPE cannot. We highly encourage you to check those out in the appendix.
This work is a wonderful insight into why positional embeddings are important. I for a long time held the beliefs that position embeddings are disturbing token embeddings and can cause misalignment. Though it is partially true, position embeddings seem to do more good than harm. The work also dives into what are some considerations to be made when deciding RoPE parameter θ. A mathematically sound and simple to understand paper explaining a core concept of current LLMs is just what the doctor ordered.
Stuffed Mamba: State Collapse and State Capacity of RNNs
TLDR:
1. Mamba/RNN based models suffer from state collapse when inferring on sequences longer than training length.
2. This is probably due to the model not forgetting initial tokens.
3. To mitigate this, one can do:
a.Decrease the retention factor for exponential decay
b.Normalise hidden states, but hurts training speed cuz non linearity
c.Reformulate hidden states, subtract the contribution of old tokens
4. This drastically improves generalisation. Mamba and its derivatives like Jamba have proved to be a worth alternative for Transformers given the latter’s memory hungry nature. If you recall, Mamba builds upon RNNs which don’t have quadratic attention complexity. They instead have a running hidden state which tries to keep track of all the information present in the sequence so far. The advantage as mentioned is you don’t need to attend to n tokens at every time step. The problem with that is, unlike transformers, it is not parallellisable for trainings.
So Mamba came up with a unique middle ground to both. What if we retain the non quadratic nature of the RNNs while also making it parallellisable for training? Well they chose Convolution to do just that. A sliding window kind of approach to process the tokens. Hence this operation attends to a local region around the current token similar to attention’s context window.
Now what is the problem you ask? Well generalisation to sequences longer than training length. If the model is trained for 8K context length, quality drops significantly immediately after 8K. They call this State Collapse (SC) You can observe the perplexity as a function of token position and this would be evident. You can also observe that the passkey retrieval accuracy falls off the cliff after 8K tokens.
This issue with generalisation beyond training length, was observed in Transformers too and it was found to be due to Position Embeddings which was hence addressed in works like YaRN etc. You can read up more about it in Eluether AI’s blog here. Now the question is, why does this happen in Mamba? Mambas don’t have position encodings because convolution is not order invariant unlike attention.
One can argue that similar to sliding window, convolution can ignore the tokens beyond the window/range. That is true but there are other components to Mamba like αt (see annotated mamba image above) which still have the information/influcent from tokens of far. Especially, at inference time, when tokens are generated sequentially discarding a lot of original information, it is hard to recreate this “sliding” nature.
Empirically it is observed that some heads going crazy can cause this. The hypothesis is that Mamba doesn’t forget the tokens enough to mimic the perfect convolutional behaviour. And it happens so because the hidden state is over parameterised aka is larger than required. This is backed by the observation that α1:t (influence of first token after t time steps) is around 0.8, which is pretty high. Also, this behaviour of poor generalisation beyond training length emerges over time and when trained on too many tokens. The bottom rows in the Figure 8 for 10B. are greenish yellow while the same are red for 40B tokens. So how do you mitigate this?
There are three approaches that the paper highlights to solve State Collapse issue. 1.Forget More and Remember Less: Well, simply increase Bt and decrease αt to decrease the impact of past tokens.
2. State Normalisation: Whenever something blows out of proportion, normalisation is the easiest trick that can help. Here we can normalise ht. But the problem is, this adds non linearity hence we cannot parallelise while training. This is a big issue.
3. Sliding Window approach: Basically formulate the hidden state to suit the sliding window behaviour. Now you essentially need to store ht, αt-r+1:t, ht-r. This would double the memory requirement for hidden state but it is alright. ht-r is the hidden state beyond the context window. Hence subtracting that essentially nullifies the influence of all the tokens that came before the current context window.
As you can see above, increasing Bt relative to αt improves generalisation. Things improve a lot more on normalisation or while enforcing sliding window structure on hidden state but Method 1 serves the purpose. The performance on downstream tasks improve significantly.
These type of works which work on pushing models to the limits and then fixing the loose ends pushes the horizons of possibility and capability. The answer generally lies in something simple and the fixes don’t generally require rewriting architectures. These are always welcome improvements.
Amortized Planning with Large-Scale Transformers: A Case Study on Chess
TLDR:
1. LLMs can learn to play chess demonstrating long term planning.
2. Each move is described by Algebraic Notation (eg: kf6 or rh8#)
3. One can train in three different variants
a. Predict score for each move. Pick the one with max score
b. Pick the state which minimises opponents winning chances
c. Emulate stockfish and pick the best move automatically.
4. The models achieve Grand Master level Elo without any tree search.A fascinating area of AI: how can machines reason and plan for long-term outcomes, much like humans do? Planning in games like chess requires thinking many moves ahead - a skill that’s tough to replicate in AI without relying on either brute force or vast memorization. In the past, approaches like Deep Q-Networks (DQN) and AlphaGo made headway by combining neural networks with search algorithms. Modern chess engines like Leela Chess Zero and Stockfish take it further, blending these techniques to make rapid, efficient moves. But here’s the big question: can neural networks go it alone, without needing those extra search algorithms?
To explore this, the team built a supervised learning dataset using 10 million games from Lichess.org (February 2023). For each position, Stockfish 16 evaluated the board’s win probability, running at max skill and depth, and spending 50ms per move. Stockfish’s centipawn scores (which show board advantage) were translated into win percentages, even marking inevitable checkmates as 100% win. This process generated an impressive 15 billion data points across all games, equating to over 24 years of single-threaded Stockfish evaluation! The test dataset, covering March 2023 games, includes around 1.8 million action-value estimates plus tricky puzzles. Some positions overlap with the training set (about 14.7%), but this was intentional to avoid distribution shifts. A specialized puzzle test set was also added, showcasing challenging board positions, each with an Elo rating and solution moves.
In training, they target three predictors - state values, action values, and oracle moves - any of which could help guide a chess policy. Their value predictors classify win probabilities into discrete "bins" (from 0% to 100%) for easier predictions, using 128 bins for state and action values. The model, a decoder-only transformer with 270 million parameters over 16 layers, tokenizes board states via FEN notation and moves in UCI format (like ‘e2e4’). For optimization, they use Adam and cross-entropy as the primary loss function.
Now, how does it decide moves? Let’s check it out for each predictor:
Action-Value predictor: This one’s all about maximizing value. It selects the move with the highest estimated value by feeding the model a combination of the tokenized current state and each possible action. In practice, it runs through all legal moves for the current state, calculates their expected values, and picks the one with the highest score.
\(\text{Loss} = −\sum_{z \in \{z_1,...z_k\}} q_i(z) \log P^{AV}θ (z|s_i,a_i), \hspace{3ex} \hat{a}^{AV}(s) = \max{a \in A_{legal}} \mathbb{E}_{Z \sim P^{AV}_θ(.|s,a)}[Z]\)State-Value predictor: Instead of just picking the highest value for itself, it aims to set up the opponent for failure in the following state. It only needs the tokenized state as input. For every possible next state s′ (reachable through legal actions), it calculates the outcome, assuming it’s now the opponent’s turn. The policy then picks the move that leads to the state with the lowest expected value for the opponent.
\(\text{Loss} = −\sum_{z \in \{z_1,...z_k\}} q_i(z) \log P^{SV}_θ (z|s_i), \hspace{3ex} \hat{a}^{SV}(s) = \min_{a \in A_{legal}} \mathbb{E}_{Z \sim P^{SV}_θ(.|s')}[Z]\)Behavioral Cloning predictor: Here, it takes a simpler approach: picking the most likely move. With the tokenized state as input, the predictor identifies the action with the highest probability based on past moves. The loss function helps reinforce this choice, training the model to go with the most probable action as determined by historical data.
\(\text{Loss} = − \log P^{BC}_θ (a^{SF}(s)|s), \hspace{3ex} \hat{a}^{BC}(s) = \max_{a \in A_{legal}} P^{BC}_θ(a|s)\)
In our value predictor equations, instead of using the standard one-hot encoding, q_i leverages something called HL-Gauss to generate a smooth categorical distribution of z_i. HL-Gauss is a histogram loss which you can learn more about here.
The results? Impressive. The models competed in tournaments to gauge Elo ratings, then faced off against other engines on Lichess. Model sizes range from 9M to 270M parameters, with the largest one reaching a grandmaster-level Elo of 2895. In a 10,000-puzzle showdown against Stockfish, GPT-3.5-turbo-instruct, AlphaZero, and Leela Chess Zero, the 270M model nearly matched AlphaZero’s search-augmented performance, excelling at puzzle-solving even without search. Performance improved as models and datasets scaled up. Although smaller datasets can lead to overfitting, this effect fades with larger data. Testing different configurations, the team found action-value prediction to be the most effective for ranking moves and solving puzzles.